문 제
APC에 온 것을 환영한다. 만약 여러분이 학교에서 자료구조를 수강했다면 해시 함수에 대해 배웠을 것이다. 해시 함수란 임의의 길이의 입력을 받아서 고정된 길이의 출력을 내보내는 함수로 정의한다. 해시 함수는 무궁무진한 응용 분야를 갖는데, 대표적으로 자료의 저장과 탐색에 쓰인다.
이 문제에서는 여러분이 앞으로 유용하게 쓸 수 있는 해시 함수를 하나 가르쳐주고자 한다. 먼저, 편의상 입력으로 들어오는 문자열에는 영문 소문자(a, b, …, z)로만 구성되어있다고 가정하자. 영어에는 총 26개의 알파벳이 존재하므로 a에는 1, b에는 2, c에는 3, …, z에는 26으로 고유한 번호를 부여할 수 있다. 결과적으로 우리는 하나의 문자열을 수열로 변환할 수 있다. 예를 들어서 문자열 “abba”은 수열 1, 2, 2, 1로 나타낼 수 있다.
해시 값을 계산하기 위해서 우리는 문자열 혹은 수열을 하나의 정수로 치환하려고 한다. 간단하게는 수열의 값을 모두 더할 수도 있다. 해시 함수의 정의에서 유한한 범위의 출력을 가져야 한다고 했으니까 적당히 큰 수 M으로 나눠주자. 짜잔! 해시 함수가 완성되었다. 이를 수식으로 표현하면 아래와 같다.
해시 함수의 입력으로 들어올 수 있는 문자열의 종류는 무한하지만 출력 범위는 정해져있다. 다들 비둘기 집의 원리에 대해서는 한 번쯤 들어봤을 것이다. 그 원리에 의하면 서로 다른 문자열이더라도 동일한 해시 값을 가질 수 있다. 이를 해시 충돌이라고 하는데, 좋은 해시 함수는 최대한 충돌이 적게 일어나야 한다. 위에서 정의한 해시 함수는 알파벳의 순서만 바꿔도 충돌이 일어나기 때문에 나쁜 해시 함수이다. 그러니까 조금 더 개선해보자.
어떻게 하면 순서가 달라졌을때 출력값도 달라지게 할 수 있을까? 머리를 굴리면 수열의 각 항마다 고유한 계수를 부여하면 된다는 아이디어를 생각해볼 수 있다. 가장 대표적인 방법은 항의 번호에 해당하는 만큼 특정한 숫자를 거듭제곱해서 곱해준 다음 더하는 것이 있다. 이를 수식으로 표현하면 아래와 같다.
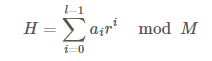
보통 r과 M은 서로소인 숫자로 정하는 것이 일반적이다. 우리가 직접 정하라고 하면 힘들테니까 r의 값은 26보다 큰 소수인 31로 하고 M의 값은 1234567891(놀랍게도 소수이다!!)로 하자.
이제 여러분이 할 일은 위 식을 통해 주어진 문자열의 해시 값을 계산하는 것이다. 그리고 이 함수는 간단해 보여도 자주 쓰이니까 기억해뒀다가 잘 써먹도록 하자.
입 력
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 10, 0 ≤ K ≤ N)
5 2
출 력
{N}{K}를 출력한다.
10
코 드
using System;
using static System.Console;
using System.IO;
namespace Algorithm
{
class Program
{
static void Main(string[] args)
{
StreamReader reader = new StreamReader(OpenStandardInput());
StreamWriter writer = new StreamWriter(OpenStandardOutput());
int wordLength = int.Parse(reader.ReadLine());
string alphabet = reader.ReadLine();
long MOD = 1234567891;
long r = 1;
long result = 0;
for (int i = 0; i < wordLength; i++)
{
result += ((long)alphabet[i] - 'a' + 1L) * r;
result = result % MOD;
r = r * 31;
r = r % MOD;
}
writer.WriteLine(result);
reader.Close();
writer.Close();
}
}
}
비교코드 - 1
공 부
DP관련 문제
1.모듈러 연산
- 나눗셈의 ‘나머지’를 계산하는 연산!
A / B = Q 와 나머지 R
A는 피제수
B는 제수
Q는 몫
R은 나머지
가끔 A를 B로 나눌 떄, ‘나머지’만 필요할 때가 있다.
이러한 경우를 위해서 ‘모듈로 연산자’ (줄여서 MOD)라 불리는 연산자가 있습니다.
위 기호 A, B, Q, R을 그대로 쓰면, ‘A mod B = R’ 가 된다.
ex)
13 / 5 = 2 나머지 3
13 mod 5 = 3
13 = 나눠지는 수, 5 = 나누는 수, 3 = 나머지
13 mod 5 = 3 mod 5 = 3
-
Q. DP에서 왜 ‘모듈러 연산’을 사용할까?
중간에 발생하는 값들이 매우 커져 정수의 표현 범위를 초과할 때 컴퓨터에서 처리할 수 있는 유효한 값으로 결과를 제한하기 위해서이다! 또한 나머지를 사용함으로써 overflow를 방지하고 계산을 효율적으로 처리할 수 있다!